2nde ∼ Interrogation n°4
Dans le repère ci-dessus les points sont à coordonnées à entières.
  1. Donner les coordonnées des points $A$, $B$, $C$ et $D$.
    2. $A(0\,;2)$ ; $B(2\,;0)$ ; $C(-3\,;-1)$ ; $D(-1\,;-3)$.
  2. Déterminer les longueur des segments $[AC]$, $[AB]$ et $[BC]$.
    3. $AC^2$ $=$ $(x_C-x_A)^2+(y_C-y_A)^2$
    $=$ $(-3-0)^2+(-1-2)^2$
    $=$ $9+9$
    $=$ $18$
    Ainsi, $AC=\sqrt{18}$ $=$ $\sqrt{9\times2}$ $=$ $\sqrt{9}\times\sqrt{2}$ $=$ $3\sqrt{2}$.
    $AB^2$ $=$ $(x_B-x_A)^2+(y_B-y_A)^2$
    $=$ $(2-0)^2+(0-2)^2$
    $=$ $4+4$
    $=$ $8$
    Ainsi, $AB=\sqrt{8}$ $=$ $\sqrt{4\times2}$ $=$ $\sqrt{4}\times\sqrt{2}$ $=$ $2\sqrt{2}$.
    $BC^2$ $=$ $(x_C-x_B)^2+(y_C-y_B)^2$
    $=$ $(-3-2)^2+(-1-0)^2$
    $=$ $25+1$
    $=$ $26$
    Ainsi, $BC=\sqrt{26}$.
  3. Le triangle $ABC$ est-il rectangle ?
    4. D'après les calculs précédents on a : $AC^2+AB^2=26=BC^2$.
    Ainsi, d'après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $A$.
  4. Calculer les coordonnées du point $P$ milieu de $[BC]$.
    5. $x_P=\dfrac{x_B+x_C}{2}$ $=$ $\dfrac{2+(-3)}{2}$ $=$ $-\dfrac{1}{2}$.

    $y_P=\dfrac{y_B+y_C}{2}$ $=$ $\dfrac{0+(-1)}{2}$ $=$ $-\dfrac{1}{2}$.

    Le point $P$ a donc pour coordonnées : $\left(-\dfrac{1}{2} \,; -\dfrac{1}{2} \right)$.
  5. Le quadrilatère $ABCD$ est-il un parallélogramme ? Un rectangle ? Un carré ?
    6. Calculons les coordonnées du milieu de $[AD]$ :

    $\left( \dfrac{x_A+x_D}{2} \,; \dfrac{y_A+y_D}{2} \right)$ $=$ $\left( \dfrac{0+(-1)}{2} \,; \dfrac{2+(-3)}{2} \right)$ $=$ $\left(-\dfrac{1}{2} \,; -\dfrac{1}{2} \right)$.

    Ainsi, les diagonales de $ABCD$ se coupent en leur milieu, c'est donc un parallélogramme.

    Or, un parallélogramme qui possède un angle droit (ici en $A$ d'après la question 3) est un rectangle.

    $ABCD$ est donc un rectangle, mais il n'est pas un carré car $AB\neq AC$.
Dans un repère du plan, les points $A$, $B$ et $C$ sont tels que $A(-3\,;2)$, $B(4\,;1)$ et $C(-2\,;3)$.
  1. Calculer les coordonnées du point $M$ tel que $A$ soit le milieu de $[BM]$.
    2. On a :
    $x_A$ $=$ $\dfrac{x_B+x_M}{2}$
    $-3$ $=$ $\dfrac{4+x_M}{2}$
    $-3\times2$ $=$ $4+x_M$
    $-6$ $=$ $4+x_M$
    $-6-4$ $=$ $x_M$
    $x_M$ $=$ $-10$.

    De plus :
    $y_A$ $=$ $\dfrac{y_B+y_M}{2}$
    $2$ $=$ $\dfrac{1+y_M}{2}$
    $2\times2$ $=$ $1+y_M$
    $4$ $=$ $1+y_M$
    $4-1$ $=$ $y_M$
    $y_M$ $=$ $3$.
    Le point $M$ a pour coordonnées $(-10\,;3)$.
  2. Calculer les coordonnées du point $N$, symétrique de $C$ par rapport à $A$.
    3. Si $N$ est le symétrique de $C$ par rapport à $A$ alors $A$ est le milieu de $[CN]$. Ainsi :
    $x_A$ $=$ $\dfrac{x_C+x_N}{2}$
    $-3$ $=$ $\dfrac{-2+x_N}{2}$
    $-3\times2$ $=$ $-2+x_N$
    $-6$ $=$ $-2+x_N$
    $-6+2$ $=$ $x_N$
    $x_N$ $=$ $-4$.

    De plus :
    $y_A$ $=$ $\dfrac{y_C+y_N}{2}$
    $2$ $=$ $\dfrac{3+y_N}{2}$
    $2\times2$ $=$ $3+y_N$
    $4$ $=$ $3+y_N$
    $4-3$ $=$ $y_N$
    $y_N$ $=$ $1$.
    Le point $N$ a pour coordonnées $(-4\,;1)$.
  3. Quelle est la nature du quadrilatère $BCMN$ ?
    4. Les diagonales de $BCMN$ ont le même milieu $A$, ainsi ce quadrilatère est un parallélogramme.
Soit $x$ un nombre réel.
Dans un repère du plan on considère les points de coordonnées $E(-4\,;\,0)$, $F(2\,;\,3)$ et $M(x\,;\,x+1)$.
  1. Montrer que $FM^2=2x^2-8x+8$ et $EM^2=2x^2+10x+17$.
    2. On a :

    $FM^2$ $=$ $(x_M-x_F)^2+(y_M-y_F)^2$
    $=$ $(x-2)^2+(x+1-3)^2$
    $=$ $(x-2)^2+(x-2)^2$
    $=$ $x^2-4x+4+x^2-4x+4$
    $=$ $2x^2-8x+8$.


    De plus :

    $EM^2$ $=$ $(x_M-x_E)^2+(y_M-y_E)^2$
    $=$ $(x+4)^2+(x+1-0)^2$
    $=$ $(x+4)^2+(x+1)^2$
    $=$ $x^2+8x+16+x^2+2x+1$
    $=$ $2x^2+10x+17$.
  2. Déterminer la valeur de $x$ pour que le triangle $EFM$ soit rectangle en $F$.
    3. Calculons tout d'abord $EF^2$ :

    $EF^2$ $=$ $(x_F-x_E)^2+(y_F-y_E)^2$
    $=$ $(2+4)^2+(3-0)^2$
    $=$ $36+9$
    $=$ $45$.


    Si on veut que le triangle $EFM$ soit rectangle en $F$, il faut, d'après le théorème de Pythagore, que :

    $EM^2$ $=$ $EF^2+FM^2$
    $2x^2+10x+17$ $=$ $45+2x^2-8x+8$
    $2x^2+10x+17$ $=$ $2x^2-8x+53$
    $2x^2+10x-2x^2+8x$ $=$ $53-17$
    $18x$ $=$ $36$
    $x$ $=$ $2$.


    Ainsi, pour que $EFM$ soit rectangle en $F$ il faut que $x=2$, soit que le point $M$ ait pour coordonnées $(2\,;\,3)$.
  3. À l'aide de votre calculatrice, expliquez comment on peut trouver une valeur approchée de $x$ pour que la distance $EM$ soit la plus petite possible. Quelle semble être cette distance minimale ?
    4. D'après la question $1$ nous avons que $EM=\sqrt{2x^2+10x+17}$.
    On saisit dans la partie 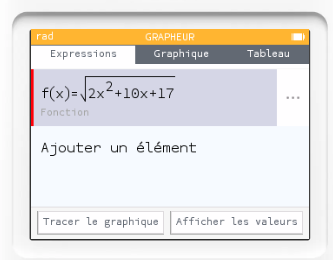fonction ou grapheur de la calculatrice cette expression algébrique On affiche ensuite le tableau associée à cette fonction. 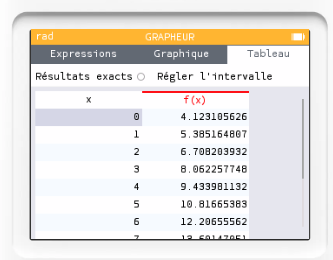On choisit "Régler l'intervalle" pour chercher la plus petite des images f(x) 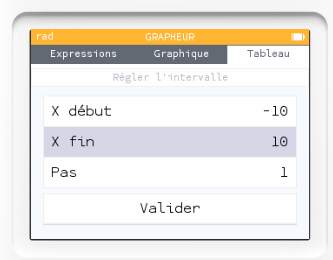On valide, et on remarque que le minimum semble être atteint entre $x=-3$ et $x=-1$. 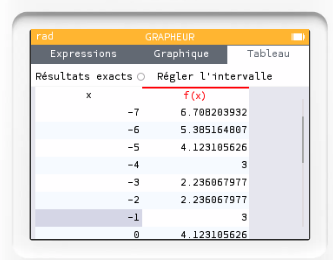On réduit ensuite le pas en réglant à nouveau l'intervalle. 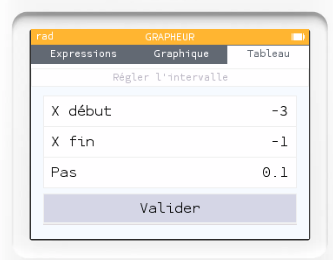Le minimum semble être atteint pour $x=-2,5$. 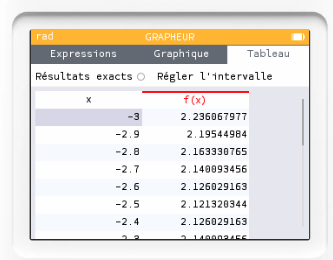On peut à nouveau régler l'intervalle pour commencer à $-2,6$ et finir à $-2,4$ avec un pas de $0,01$ pour vérifier cette affirmation.

    La distance minimale semble donc être atteinte pour $x=-2,5$ et elle vaut : $\sqrt{2\times(-2,5)^2+10\times(-2,5)+17}$ $=$ $\sqrt{4,5}$ $=$ $\dfrac{3\sqrt{2}}{2}$.